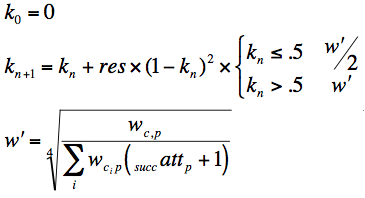Difference between revisions of "CUMULATE asymptotic knowledge assessment"
| (5 intermediate revisions by the same user not shown) | |||
| Line 14: | Line 14: | ||
=Examples= | =Examples= | ||
| − | Below is a graph of concept's knowledge level growth vs. number of successful attempts to apply it | + | Below is a graph of concept's knowledge level growth vs. number of successful attempts to apply it. Every time the concept is applied correctly in a new problem. Every time the concept is the only concept of the problem. Namely, the ''Wc,p''/Σ''Wc,p'' ratio is equal to 1. |
| + | |||
[[Image:CUMULATE asymptotic knowledge assessment - knowledge growth.png]] | [[Image:CUMULATE asymptotic knowledge assessment - knowledge growth.png]] | ||
| Line 22: | Line 23: | ||
The major drawback of the above [[CUMULATE asymptotic knowledge assessment|asymptotic knowledge assessment]] algorithm is that it is intended to be used as ''one-fits-all'' method not suitable for parametrization. Namely: | The major drawback of the above [[CUMULATE asymptotic knowledge assessment|asymptotic knowledge assessment]] algorithm is that it is intended to be used as ''one-fits-all'' method not suitable for parametrization. Namely: | ||
* the initial knowledge level (''Ko'') can only start from 0 | * the initial knowledge level (''Ko'') can only start from 0 | ||
| − | * the speed of knowledge growth cannot be adjusted (slow for hard concepts, fast for easy concepts) | + | * the speed of knowledge growth cannot be adjusted (e.g. slow for hard concepts, fast for easy concepts) |
* problem repetition penalty is not adjustable as well | * problem repetition penalty is not adjustable as well | ||
| − | As a result | + | As a result modeling is done in the same way for all users solving all problems. No special attention is given to individual user differences and individual problem complexity. |
| + | |||
| + | One of the ways to overcome these shortcomings is an attempt to create a [[CUMULATE parametrized asymptotic knowledge assessment|parameterizable]] version of this algorithm. | ||
| − | + | = Contacts = | |
| + | [[User:Myudelson | Michael V. Yudelson]] | ||
Latest revision as of 23:16, 8 April 2009
Asymptotic knowledge assessment is CUMULATE's legacy user modeling algorithm for computing user knowledge with respect to problem-solving.
Contents
Computation
The formula below is used to update the knowledge levels of concepts (c) addressed in a problem (p). This formula reflects the following principles.
- there are several domain concepts (knowledge items, rules, productions) involved in solving a problem; the knowledge of each of them is updated proportionally to the others
- knowledge is updated only upon correct user answers, there is no penalty for errors
- solving a problem correctly multiple times will result in diminishing update (growth) of the knowledge level of the concepts as the number of successes grows
- Ko - is the starting level of knowledge (here we always start from 0)
- res - result of user action (0 -error, 1 - correct);
- Wc,p - is a weight of concept c in problem p
- ΣWc,p - is the sum of weights of all concepts in problem p
- succattp - is a number of successful solutions to problem p prior to current attempt
Examples
Below is a graph of concept's knowledge level growth vs. number of successful attempts to apply it. Every time the concept is applied correctly in a new problem. Every time the concept is the only concept of the problem. Namely, the Wc,p/ΣWc,p ratio is equal to 1.
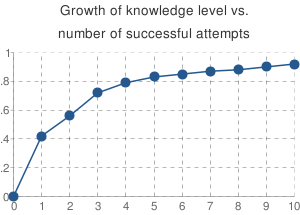
(alternatively via Google Chart API)
Criticism
The major drawback of the above asymptotic knowledge assessment algorithm is that it is intended to be used as one-fits-all method not suitable for parametrization. Namely:
- the initial knowledge level (Ko) can only start from 0
- the speed of knowledge growth cannot be adjusted (e.g. slow for hard concepts, fast for easy concepts)
- problem repetition penalty is not adjustable as well
As a result modeling is done in the same way for all users solving all problems. No special attention is given to individual user differences and individual problem complexity.
One of the ways to overcome these shortcomings is an attempt to create a parameterizable version of this algorithm.