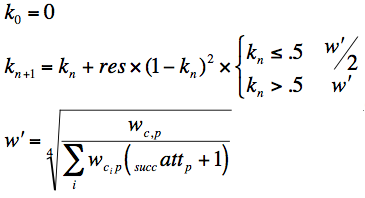CUMULATE asymptotic knowledge assessment
Asymptotic knowledge assessment is CUMULATE's legacy user modeling algorithm for computing user knowledge with respect to problem-solving.
Contents
Computation
The formula below is used to update the knowledge levels of concepts (c) addressed in a problem (p). This formula reflects the following principles.
- there are several domain concepts (knowledge items, rules, productions) involved in solving a problem; the knowledge of each of them is updated proportionally to the others
- knowledge is updated only upon correct user answers, there is no penalty for errors
- solving a problem correctly multiple times will result in diminishing update (growth) of the knowledge level of the concepts as the number of successes grows
- Ko - is the starting level of knowledge (here we always start from 0)
- res - result of user action (0 -error, 1 - correct);
- Wc,p - is a weight of concept c in problem p
- ΣWc,p - is the sum of weights of all concepts in problem p
- succattp - is a number of successful solutions to problem p prior to current attempt
Examples
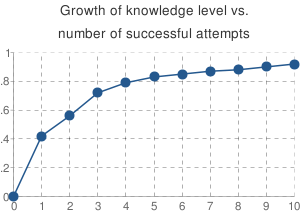
Below is a graph of concept's knowledge level growth vs. number of successful attempts to apply it. Every time the concept is applied correctly in a new problem. Every time the concept is the only concept of the problem. Namely, the Wc,p/ΣWc,p ratio is equal to 1.
(alternatively via Google Chart API)
Criticism
The major drawback of the above asymptotic knowledge assessment algorithm is that it is intended to be used as one-fits-all method not suitable for parametrization. Namely:
- the initial knowledge level (Ko) can only start from 0
- the speed of knowledge growth cannot be adjusted (e.g. slow for hard concepts, fast for easy concepts)
- problem repetition penalty is not adjustable as well
As a result modeling is done in the same way for all users solving all problems. No special attention is given to individual user differences and individual problem complexity.
One of the ways to overcome these shortcomings is an attempt to create a parameterizable version of this algorithm.