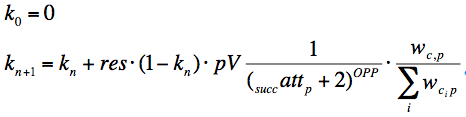Difference between revisions of "CUMULATE parametrized asymptotic knowledge assessment"
m (→Example 1) |
m (→Example 1) |
||
| Line 25: | Line 25: | ||
* the red line ''merges'' the two graphs above | * the red line ''merges'' the two graphs above | ||
| − | [[Image:CUMULATE parameterized asymptotic knowledge assessment - knowledge growth and penalty.png]] | + | [[Image:CUMULATE parameterized asymptotic knowledge assessment - knowledge growth and penalty.png|thumb]] |
<br/>([http://chart.apis.google.com/chart?cht=lxy&chs=300x240&chd=t:0,10,20,30,40,50,60,70,80,90,100|00,50,75,88,94,97,98,99,100,100,100|-1|-1,100,84,76,71,67,64,61,59,58,56|-1|00,50,63,66,66,65,63,61,59,58,56&chco=24588E,4C9B46,CF1E2B&chxt=x,y&chxl=1:|0|.2|.4|.6|.8|1|0:|0|1|2|3|4|5|6|7|8|9|10&chm=o,24588E,0,-1,10|o,4C9B46,1,-1,10|o,CF1E2B,2,-1,10&chg=10,20&chdl=knowledge+level|penalty+coefficient|resulting+curve&chdlp=b+&chls=1,1,0|1,1,0|3,6,3&chtt=Knowledge+level+growth+and+change+in+penalty|coefficient+vs.+number+of+successful+attempts&chdlp=b alternatively] via [http://code.google.com/apis/chart/ Google Chart API]) | <br/>([http://chart.apis.google.com/chart?cht=lxy&chs=300x240&chd=t:0,10,20,30,40,50,60,70,80,90,100|00,50,75,88,94,97,98,99,100,100,100|-1|-1,100,84,76,71,67,64,61,59,58,56|-1|00,50,63,66,66,65,63,61,59,58,56&chco=24588E,4C9B46,CF1E2B&chxt=x,y&chxl=1:|0|.2|.4|.6|.8|1|0:|0|1|2|3|4|5|6|7|8|9|10&chm=o,24588E,0,-1,10|o,4C9B46,1,-1,10|o,CF1E2B,2,-1,10&chg=10,20&chdl=knowledge+level|penalty+coefficient|resulting+curve&chdlp=b+&chls=1,1,0|1,1,0|3,6,3&chtt=Knowledge+level+growth+and+change+in+penalty|coefficient+vs.+number+of+successful+attempts&chdlp=b alternatively] via [http://code.google.com/apis/chart/ Google Chart API]) | ||
Revision as of 21:36, 20 January 2010
CUMULATE's parameterized asymptotic knowledge assessment algorithm is an attempt to overcome shortcomings of its non-paramterized version. Namely, one-fits-all nature, prohibiting parameter tuning for individual users' abilities and problem complexities.
Computation
The formula below is used to update the knowledge levels of concepts (c) addressed in a problem (p). This formula reflects the following principles (identical to the predecessor algorithm).
- there are several domain concepts (knowledge items, rules, productions) involved in solving a problem; the knowledge of each of them is updated proportionally to the others
- knowledge is updated only upon correct user answers, there is no penalty for errors
- solving a problem correctly multiple times will result in diminishing update (growth) of the knowledge level of the concepts as the number of successes grows
in addition:
- the initial level of knowledge, speed of knowledge growth, and penalty for repetitive (correct) solutions to the problem - are now adjustable parameters
- Ko - is the starting level of knowledge, Ko ∈ [0, 1]
- res - result of user action (0 -error, 1 - correct);
- Wc,p - is a weight of concept c in problem p
- ΣWc,p - is the sum of weights of all concepts in problem p
- succattp - is a number of successful solutions to problem p prior to current attempt
- pV - speed of knowledge growth parameter, pV ∈ [0, 1]
- OPP - over-practicing parameter, controlling the penalty for repetitively solving one problem (correctly), OPP ∈ [0, 1]
Examples
Example 1
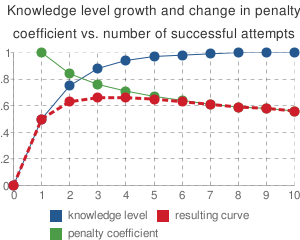
Below is a graph of concept's knowledge level growth and the penalty coefficient vs. number of successful attempts to apply it in a problem. The lines denote:
- the blue line denotes a successful use of a concept in a new problem (pV = .5)
- the green line denotes a penalty coefficient -- 1/(succattp+2)OPP -- as if it was the same problem (OPP = .25)
- the red line merges the two graphs above
(alternatively via Google Chart API)
Example 2
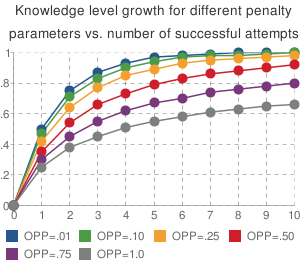
Below the speed of problem learning is held constant (pV = .5) while the penalty for practicing the same problem changes.
(alternatively via Google Chart API)
Example 3
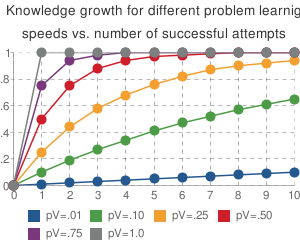
Graph below shows differences the growth of knowledge while speed of learning varies. No penalty is given.
(alternatively via Google Chart API)
Studies
- Study 1 - comparison of the legacy and parametrized algorithms based on SQL problem-solving data